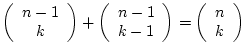| Back | |||||
|
PDF Version (70 KB)
Bézier Curves
Urs Oswald osurs@bluewin.ch http://www.ursoswald.ch September 11, 2002
Quadratic Bézier curves
From the above equations, it follows that
Cubic Bézier curves
From (2), we get
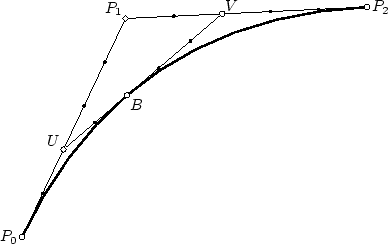
From (1), In fig. 2, if
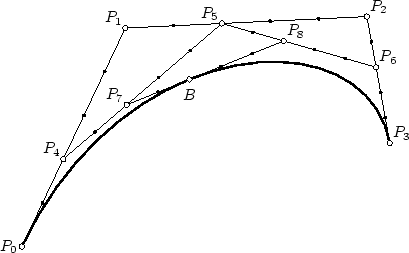
Bézier curves of arbitrary order
For distinct points
Theorem 1 (Bézier curves of order 1)
For points
PROOF: By the above definition,
Theorem 2
For any non-negative integer
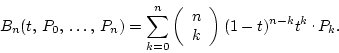
PROOF: By induction on 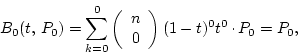
which is correct by the first part of the definition. For ![\begin{displaymath}
(1-t)\left[
\sum_{k=0}^{n-1}\left(\begin{array}{c}n-1\ k...
...\right)(1-t)^{n-1-k}t^k\raisebox{.5ex}{ . }P_{k+1}
\right].
\end{displaymath}](img42.png)
We get
| |||||
|
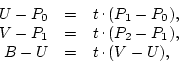
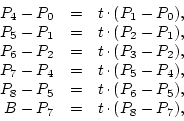
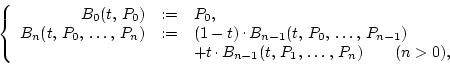
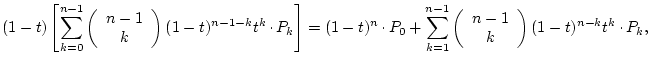
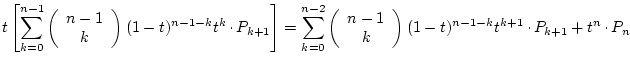
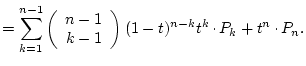
![$\displaystyle
B_n(t, P_0, \dots, P_n)=
(1-t)^n\raisebox{.5ex}{ . }P_0
+...
...\right] (1-t)^{n-k}t^k\raisebox{.5ex}{ . }P_k
+t^n\raisebox{.5ex}{ . }P_n
$](img46.png)
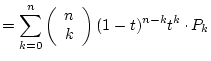 , as
, as